GALILEI – Giornata Terza – de motu locali

Traduz. Ciro A. R. Abilitato

GALILEO GALILEI

DISCORSI E DIMOSTRAZIONI MATEMATICHE
INTORNO A DUE NUOVE SCIENZE
ATTENENTI ALLA MECANICA & I MOVIMENTI LOCALI
In Leida, Appresso gli Elzevirii. M.D.C.XXXVIII

GIORNATA TERZA

DE MOTU LOCALI
De subiecto vetustissimo novissimam promovemus scientiam. MOTU nil forte antiquius in natura, et circa eum volumina nec pauca nec parva a philosophis conscripta reperiuntur; symptomatum tamen, quae complura et scitu digna insunt in eo, adhuc inobservata, necdum indemonstrata, comperio. Leviora quaedam adnotantur, ut, gratia exempli, naturalem motum gravium descendentium continue accelerari; verum, iuxta quam proportionem eius fiat acceleratio, proditum hucusque non est: nullus enim, quod sciam, demonstravit, spatia a mobili descendente ex quiete peracta in temporibus aequalibus, eam inter se retinere rationem, quam habent numeri impares ab unitate consequentes. Observatum est, missilia, seu proiecta, lineam qualitercunque curvam designare; veruntamen, eam esse parabolam, nemo prodidit. Haec ita esse, et alia non pauca nec minus scitu digna, a me demonstrabuntur, et, quod pluris faciendum censeo, aditus et accessus ad amplissimam praestantissimamque scientiam, cuius hi nostri labores erunt elementa, recludetur, in qua ingenia meo perspicaciora abditiores recessus penetrabunt.
Tripartito dividimus hanc tractationem: in prima parte consideramus ea quae spectant ad motum aequabilem, seu uniformem; in secunda de motu naturaliter accelerato scribimus; in tertia, de motu violento, seu de proiectis.

DE MOTU AEQUABILI
Circa motum aequabilem, seu uniformem, unica opus habemus definitione, quam eiusmodi profero:

DEFINITIO.
Aequalem, seu uniformem, motum intelligo eum, cuius partes quibuscunque temporibus aequalibus a mobili peractae, sunt inter se aequales.

ADMONITIO.
Visum est addere veteri definitioni (quae simpliciter appellat motum aequabilem, dum temporibus aequalibus aequalia transiguntur spatia) particulam quibuscunque, hoc est omnibus temporibus aequalibus: fieri enim potest, ut temporibus aliquibus aequalibus mobile pertranseat spatia aequalia, dum tamen spatia transacta in partibus eorundem temporum minoribus, licet aequalibus, aequalia non sint. Ex allata definitione quatuor pendent axiomata, scilicet:

AXIOMA I.
Spatium transactum tempore longiori in eodem motu aequabili maius esse spatio transacto tempore breviori.

AXIOMA II.
Tempus quo maius spatium conficitur in eodem motu aequabili, longius est tempore quo conficitur spatium minus.

AXIOMA III.
Spatium a maiori velocitate confectum tempore eodem, maius est spatio confecto a minori velocitate.

AXIOMA IV.
Velocitas qua tempore eodem conficitur maius spatium, maior est velocitate, qua conficitur spatium minus.

THEOREMA I. PROPOSITIO I.
Si mobile aequabiliter latum eademque cum velocitate duo pertranseat spatia, tempora lationum erunt inter se ut spatia peracta.

Pertranseat enim mobile aequabiliter latum eadem cum velocitate duo spatia AB, BC, et sit tempus motus per AB, DE; tempus vero motus per BC esto EF: dico, ut spatium AB ad spatium BC, ita esse tempus DE ad tempus EF. Protrahantur utrinque spatia et tempora versus G, H et I, K, et in AG sumantur quotcunque spatia ipsi AB aequalia, et totidem tempora in DI, tempori DE, similiter aequalia; et rursus in CH sumantur secundum quamcunque multitudinem spatia ipsi CB aequalia, et totidem tempora in FK, tempori EF aequalia: erunt iam spatium BG et tempus EI aeque multiplicia spatii BA et temporis ED iuxta quamcunque multiplicationem accepta, et similiter spatium HB et tempus KE spatii CB temporisque FE aeque multiplicia in qualibet multiplicatione. Et quia DE est tempus lationis per AB, erit totum EI tempus totius BG, cum motus ponatur aequabilis sintque in EI tot tempora ipsi DE aequalia quot sunt in BG spatia aequalia BA; et similiter concludetur, KE esse tempus lationis per HB. Cum autem motus ponatur aequabilis, si spatium GB esset aequale ipsi BH, tempus quoque IE tempori EK foret aequale; et si GB maius sit quam BH, etiam IE quam EK maius erit; et si minus, minus. Sunt itaque quatuor magnitudines, AB prima, BC secunda, DF tertia, EF quarta, et primae et tertiae, nempe spatii AB et temporis DE, sumpta sunt aeque multiplicia iuxta quamcunque multiplicationem tempus IE et spatium GB; ac demonstratum est, haec vel una aequari, vel una deficere, vel una excedere, tempus EK et spatium BH, aeque multiplicia scilicet secundae at quartae: ergo prima ad secundam, nempe spatium AB ad spatium BC, eadem habet rationem quam tertia et quarta, nempe tempus DE ad tempus EF: quod erat demonstrandum.

GALILEO GALILEI

DISCORSI E DIMOSTRAZIONI MATEMATICHE
INTORNO A DUE NUOVE SCIENZE
ATTENENTI ALLA MECANICA & I MOVIMENTI LOCALI
In Leida, Appresso gli Elzevirii. M.D.C.XXXVIII

TERZA GIORNATA

DEL MOTO LOCALE
Diamo avvio a una nuovissima scienza intorno ad un soggetto antichissimo. Rispetto al MOTO non v’è forse in natura nulla di più antico, e intorno ad esso né pochi volumi si trovano, né di piccola mole che siano stati scritti dai filosofi; ciononostante, tra le sue espressioni proprie, delle quali in esso ve ne sono di degne da essere conosciute, ne trovo molte rimaste fino ad ora inosservate e non ancora dimostrate. Se ne rilevano alcune più immediate, come quella, per esempio, che il moto naturale dei gravi discendenti è continuamente accelerato; però, secondo quale proporzione del medesimo l’accelerazione avvenga, non è stato sin qui dimostrato: nessuno, che io sappia, infatti, ha dimostrato che gli spazi percorsi in tempi eguali da un mobile discendente, intrattengono tra loro quella stessa proporzione che hanno i numeri impari successivi all’unità. È stato osservato che i corpi da getto, ovverossia i proietti, descrivono una linea curva di un qualche tipo; pur tuttavia, che essa sia una parabola, nessuno l’ha evidenziato. Che le cose stiano così, verrà da me dimostrato insieme a non poche altre cose, né meno degne d’essere conosciute, e, ciò che stimo ancor più importante, si apriranno possibilità di accesso ad una vastissima e importantissima scienza, di cui queste nostre ricerche costituiranno gli elementi, e nella quale ingegni più acuti del mio penetreranno poi i più ascosi recessi.
Dividiamo questa trattazione in tre parti: nella prima parte consideriamo le particolarità che attengono al moto equabile o, se si vuole, uniforme; nella seconda trattiamo del moto naturalmente accelerato; nella terza del moto violento, ossia dei proietti.

DEL MOTO EQUABILE
Circa il moto equabile, ovvero uniforme, ci si rende necessaria una sola definizione, che in tal modo formulo:

DEFINIZIONE
Per moto equale o uniforme intendo quello in cui gli spazi percorsi da un mobile in tempi eguali qualsiasi [in qualsiasi modo presi], sono tra di loro eguali.

AVVERTENZA
È parso opportuno aggiungere alla vecchia definizione (che semplicemente chiama equabile il moto, fintanto che in tempi eguali vengono attraversati spazi eguali) la parte di frase ‘qualsiasi [di qualsiasi estensione]’, cioè per tutti i tempi eguali: infatti, può accadere che in determinati tempi eguali un mobile percorra spazi eguali, mentre spazi attraversati in frazioni minori dei medesimi tempi, quantunque eguali, non siano eguali. Dalla precedente definizione dipendono quattro assiomi, cioè:

ASSIOMA I
Lo spazio attraversato in un tempo più lungo durante uno stesso moto equabile, è maggiore dello spazio attraversato in un tempo più breve.

ASSIOMA II
Il tempo nel quale durante uno stesso moto equabile viene percorso uno spazio maggiore, è più lungo del tempo impiegato a percorrere uno spazio minore.

ASSIOMA III
In uno stesso tempo, lo spazio percorso a velocità maggiore è maggiore di quello percorso a velocità minore.

ASSIOMA IV
In uno stesso tempo, la velocità alla quale viene percorso uno spazio maggiore è maggiore di quella alla quale viene percorso uno spazio minore.

TEOREMA I. PROPOSIZIONE I
Se un mobile, dotato di moto equabile, attraversa due spazi con la stessa velocità, i tempi dei moti staranno tra di loro come gli spazi percorsi.

Un mobile dotato di moto equabile attraversi infatti con la stessa velocità due spazi AB e BC, e sia il tempo del moto per AB, DE; di certo il tempo del moto per BC sarà EF: dico che lo spazio AB sta allo spazio BC, come il tempo DE sta al tempo EF. Si prolunghino dall’una e dall’altra parte gli spazi e i tempi verso G e H e verso I e K, e in AG si prendano gli stessi spazi ad AB eguali, qualunque sia il loro numero, e altrettanti tempi in DI, similmente eguali al tempo DE; e dall’altra parte, si prendano in CH, in qualsiasi numero, gli stessi spazi a CB eguali, e altrettanti tempi in FK, eguali al tempo EF: lo spazio BG e il tempo EI saranno allora in ugual misura multipli dello spazio BA e del tempo ED secondo qualsivoglia moltiplicazione, e similmente lo spazio HB e il tempo KE, lo spazio CB e il tempo FE saranno in ugual misura multipli secondo qualsiasi moltiplicazione. E poiché DE è il tempo del transito per AB, EI sarà tutto il tempo dell’intero BG, allorché si ponga un moto equabile e ci siano in EI tanti tempi eguali allo stesso DE, quanti spazi ci sono in BG eguali a BA; e similmente si conclude dicendo che KE è il tempo del transito per HB. Quando d’altra parte si ponga un moto equabile, se lo spazio GB fosse eguale allo stesso BH, anche il tempo IE sarebbe eguale al tempo EK; e se GB fosse maggiore di BH, anche IE sarebbe maggiore di EK; e se minore, minore. Ci sono pertanto quattro quantità, AB la prima, BC la seconda, DE la terza, EF la quarta, e della prima e della terza, AB naturalmente riguardante lo spazio e DE il tempo, mentre sono presi come multipli uguali secondo qualunque moltiplicazione il tempo IE e lo spazio GB; ma è per queste dimostrato che o insieme eguagliano, o insieme non raggiungono, o insieme eccedono il tempo EK e lo spazio BH, multipli eguali, evidentemente, della seconda e della quarta: dunque la prima sta alla seconda, e certamente lo spazio AB allo spazio BC, e la stessa relazione si ha con la terza e la quarta, e certamente il tempo DE al tempo EF: ciò è quanto era da dimostrare.

THEOREMA II. PROPOSITIO II.
Si mobile temporibus aequalibus duo pertranseat spatia, erunt ipsa spatia inter se ut velocitates. Et si spatia sint ut velocitates, tempora erunt aequalia.

Assumpta enim superiori figura, sint duo spatia AB, BC transacta aequalibus temporibus, spatium quidem AB cum velocitate DE, et spatium BC cum velocitate EF: dico, spatium AB ad spatium BC esse ut DE velocitas ad velocitatem EF. Sumptis enim utrinque, ut supra, et spatiorum et velocitatum aeque multiplicibus secundum quamcunque multiplicationem, scilicet GB et IE ipsorum AB et DE, pariterque HB, KE ipsorum BC, EF, concludetur, eodem modo ut supra, multiplicia GB, IE vel una deficere, vel aequari, vel excedere, aeque multiplicia BH, EK. Igitur et manifestum est propositum.

TEOREMA II. PROPOSIZIONE II
Se un mobile percorre due spazi in tempi eguali, i medesimi spazi staranno tra loro come le velocità. E se gli spazi stanno come le velocità, i tempi saranno eguali.

Facendo infatti riferimento alla figura posta più in alto [precedente], siano AB e BC due spazi attraversati in tempi eguali, lo spazio AB appunto con la velocità DE, e lo spazio BC alla velocità EF: sostengo che lo spazio AB sta allo spazio BC come la velocità DE sta alla velocità EF. Presi infatti dall’una e dall’altra parte, come sopra, sia per gli spazi che per le velocità, e ugualmente mediante multipli secondo qualunque moltiplicazione, appunto GB e IE degli stessi AB e DE, e parimenti HB e KE degli stessi BC e EF, si concluderà nel medesimo modo di sopra, che cioè i multipli GB e IE o insieme non raggiungono, o insieme eguagliano, o insieme ugualmente eccedono i multipli BH e EK. Da ciò è resa evidente la premessa.

THEOREMA III. PROPOSITIO III.
Inaequalibus velocitatibus per idem spatium latorum tempora, velocitatibus e contrario respondent.

Sint velocitates inaequales A maior, B minor, et secundum utramque fiat motus per idem spatium CD: dico, tempus quo A velocitas permeat spatium CD, ad tempus quo velocitas B idem spatium permeat, esse ut velocitas B ad velocitatem A. Fiat enim ut A ad B, ita CD ad CE; erit igitur, ex praecedenti, tempus, quo A velocitas conficit CD, idem cum tempore quo B conficit CE: sed tempus quo velocitas B conficit CE, ad tempus quo eadem conficit CD, est ut CE ad CD; ergo tempus quo velocitas A conficit CD, ad tempus quo velocitas B idem CD conficit, est ut CE ad CD, hoc est ut velocitas B ad velocitatem A: quod erat intentum.

TEOREMA III. PROPOSIZIONE III
A velocità diseguali, i tempi degli spostamenti attraverso uno stesso spazio presentano corrispondenza inversa rispetto alle velocità.

Siano A e B velocità diseguali, una maggiore e una minore, e si produca secondo l’una e l’altra un moto attraverso lo stesso spazio CD: sostengo che il tempo in cui la velocità A attraversa lo spazio CD sta al tempo in cui la velocità B attraversa il medesimo spazio, come la velocità B sta alla velocità A. Si ponga infatti che A stia a B come CD sta a CE; quindi, dal precedente, il tempo in cui la velocità A percorre CD sarà lo stesso del tempo in cui B percorre CE: ma il tempo in cui la velocità B copre CE sta al tempo in cui la stessa copre CD, come sta CE a CD; dunque il tempo in cui la velocità A percorre CD sta al tempo in cui la velocità B percorre lo stesso CD, come CE sta a CD, cioè a dire come la velocità B sta alla velocità A: ciò è quanto volevasi stabilire.

THEOREMA IV. PROPOSITIO IV.
Si duo mobilia ferantur motu aequabili, inaequali tamen velocitate, spatia temporibus inaequalibus ab ipsis peracta habebunt rationem compositam ex ratione velocitatum et ex ratione temporum.

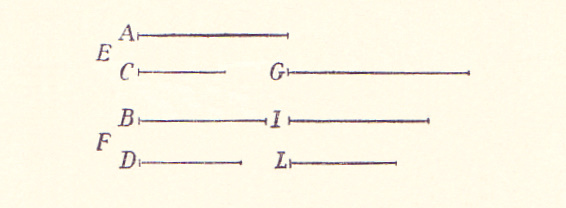
Mota sint duo mobilia E, F motu aequabili, et ratio velocitatis mobilis E ad velocitatem mobilis F sit ut A ad B; temporis vero quo movetur E, ad tempus quo movetur F, ratio sit ut C ad D: dico, spatium peractum ab E cum velocitate A in tempore C, ad spatium peractum ab F cum velocitate B in tempore D, habere rationem compositam ex ratione velocitatis A ad velocitatem B et ex ratione temporis C ad tempus D. Sit spatium ad E cum velocitate A in tempore C peractum G, et ut velocitas A ad velocitatem B, ita fiat G ad I; ut autem tempus C ad tempus D, ita sit I ad L: constat, I esse spatium quo movetur F in tempore eodem in quo E motum est per G, cum spatia G, I sint ut velocitates A, B. Et cum sit ut tempus C ad tempus D, ita I ad L: sit autem I spatium quod conficitur a mobili F in tempore C; erit L spatium quod conficitur ab F in tempore D cum velocitate B. Ratio autem G ad L componitur ex rationibus G ad I et I ad L, nempe ex rationibus velocitatis A ad velocitatem B et temporis C ad tempus D: ergo patet propositum.

TEOREMA IV. PROPOSIZIONE IV
Se due mobili si muovono di moto equabile, e però con diseguale velocità, gli spazi da essi percorsi in tempi diseguali si troveranno in un rapporto di proporzionalità che sarà composto dalla proporzione tra le velocità e dalla proporzione tra i tempi.

Che due mobili E e F siano mossi con moto equabile, e il rapporto di proporzionalità della velocità del mobile E rispetto alla velocità del mobile F sia come A rispetto a B; inoltre, il rapporto di proporzionalità del tempo nel quale si muove E rispetto al tempo nel quale si muove F sia come C rispetto a D: affermo che lo spazio percorso da E alla velocità A nel tempo C, sta allo spazio percorso da F alla velocità B nel tempo D, secondo un rapporto di proporzionalità composto dal rapporto della velocità A rispetto alla velocità B e dal rapporto del tempo C rispetto al tempo D. Sia G, riguardo ad E, lo spazio percorso alla velocità A nel tempo C, e si ammetta che come la velocità A sta alla velocità B, così G stia ad I; come poi il tempo C sta al tempo D, così sia I rispetto a L: risulta che I è lo spazio per cui si muove F nel medesimo tempo in cui il moto E si produce attraverso G, poiché gli spazi G e I stanno come le velocità A e B. E, a condizione che come il tempo C sta al tempo D, così I stia ad L, sia poi I lo spazio che viene percorso dal mobile F nel tempo C; L sarà allora lo spazio che verrà percorso da F nel tempo D alla velocità B. Ora, il rapporto di G rispetto a L si compone della proporzione dei rapporti di G rispetto a I e di I rispetto a L, cioè appunto della proporzione dei rapporti della velocità A rispetto alla velocità B e del tempo C rispetto al tempo D: è dunque così spiegata la proposizione.

THEOREMA V. PROPOSITIO V.
Si duo mobilia aequabili motu ferantur, sint tamen velocitates inaequales, et inaequalia spatia peracta, ratio temporum composita erit ex ratione spatiorum et ex ratione velocitatum contrarie sumptarum.

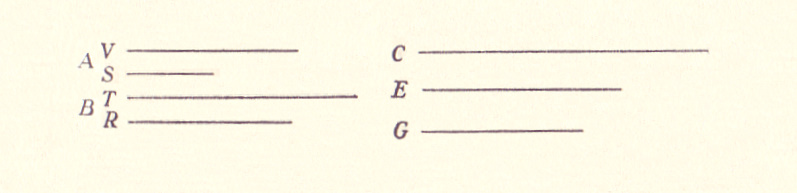
Sint duo mobilia A, B, sitque velocitas ipsius A ad velocitatem ipsius B ut V ad T; spatia autem peracta sint ut S ad R: dico, rationem temporis quo motum est A, ad tempus quo motum est B, compositam esse ex ratione velocitatis T ad velocitatem V et ex ratione spatii S ad spatium R. Sit ipsius motus A tempus C, et ut velocitas T ad velocitatem V, ita sit tempus C ad tempus E; et cum C sit tempus in quo A cum velocitate V conficit spatium S, sitque ut velocitas T mobilis B ad velocitatem V, ita tempus C ad tempus E, erit tempus E illud in quo mobile B conficeret idem spatium S. Fiat modo ut spatium S ad spatium R, ita tempus E ad tempus G: constat, G esse tempus quo B conficeret spatium R. Et quia ratio C ad G componitur ex rationibus C ad E et E ad G; est autem ratio C ad E eadem cum ratione velocitatum mobilium A, B contrarie sumptarum, hoc est cum ratione T ad V; ratio vero E ad G est eadem cum ratione spatiorum S, R; ergo patet propositum.

TEOREMA V. PROPOSIZIONE V
Se due mobili si muovono di moto equabile, e però le loro velocità siano diseguali, come anche diseguali siano gli spazi percorsi, il rapporto di proporzionalità tra i tempi risulterà composto dalla proporzione tra gli spazi e dalla proporzione tra le velocità inversamente poste.

Siano A e B due movibili, e sia la velocità di esso A rispetto alla velocità di esso B come V sta a T; gli spazi percorsi siano invece come S sta a R: sostengo che il rapporto del tempo in cui si ha il moto di A, rispetto al tempo in cui si ha il moto di B, si compone del rapporto della velocità T rispetto alla velocità V, e del rapporto dello spazio S rispetto allo spazio R. Sia C il tempo di esso moto A, e come la velocità T sta alla velocità V, così sia per il tempo C rispetto al tempo E; e poiché C è il tempo in cui A alla velocità V percorre lo spazio S, e dato che come la velocità T del mobile B sta alla velocità V, così il tempo C sta al tempo E, allora il tempo E sarà quello nel quale esso spazio S sarà percorso dal mobile B. Si ponga ora che come lo spazio S sta allo spazio R, così il tempo E stia al tempo G: risulta che G è il tempo in cui B percorre lo spazio R. E poiché il rapporto C a G si compone del prodotto dei rapporti C a E e E a G; mentre il rapporto C a E è identico al rapporto delle velocità dei mobili A e B inversamente poste, cioè al rapporto T a V; allora in realtà il rapporto E a G è identico al rapporto degli spazi S e R; così dunque la proposizione è spiegata.

THEOREMA VI. PROPOSITIO VI.
Si duo mobilia aequabili motu ferantur, ratio velocitatum ipsorum composita erit ex ratione spatiorum peractorum et ex ratione temporum contrarie sumptorum.

Sint duo mobilia A, B, aequabili motu lata; sint autem spatia ab illis peracta in ratione V ad T, tempora vero sint ut S ad R: dico, velocitatem mobilis A ad velocitatem ipsius B habere rationem compositam ex ratione spatii V ad spatium T et temporis R ad tempus S.
Sit velocitas C ea cum qua mobile A conficit spatium V in tempore S, et quam rationem habet spatium V ad spatium T, hanc habeat velocitas C ad aliam E; erit E velocitas cum qua mobile B conficit spatium T in tempore eodem S: quod si fiat, ut tempus R ad tempus S, ita velocitas E ad aliam G, erit velocitas G illa secundum quam mobile B conficit spatium T in tempore R. Habemus itaque velocitatem C, cum qua mobile A conficit spatium V in tempore S, et velocitatem G, cum qua mobile B conficit spatium T in tempore R, et est ratio C ad G composita ex rationibus C ad E et E ad G; ratio autem C ad E posita est eadem cum ratione spatii V ad spatium T; ratio vero E ad G est eadem cum ratione R ad S: ergo patet propositum.

TEOREMA VI. PROPOSIZIONE VI
Se due mobili si muovono di moto equabile, il rapporto di proporzionalità tra le loro velocità risulterà composto dalla proporzione tra gli spazi percorsi e dalla proporzione tra i tempi inversamente presi.

Siano A e B due movibili che scorrono con moto equabile; stiano poi gli spazi da questi percorsi nel rapporto V a T, i tempi stiano inoltre come S sta a R: affermo che la velocità del mobile A rispetto alla velocità del suo pari B presenta un rapporto di proporzionalità composto dal prodotto dei rapporti dello spazio V rispetto allo spazio T e del tempo R rispetto al tempo S.
Sia C la velocità alla quale il mobile A percorre lo spazio V nel tempo S, mentre quale proporzione mostri lo spazio V rispetto allo spazio T, la stessa abbia la velocità C rispetto all’altra E; E sarà allora la velocità alla quale il mobile B percorre lo spazio T nello stesso tempo S: per la qual ragione si ponga che come il tempo R sta al tempo S, così la velocità E stia all’altra G, sarà allora la velocità G quella secondo la quale il mobile B percorre lo spazio T nel tempo R. Abbiamo pertanto la velocità C, alla quale il mobile A percorre lo spazio V nel tempo S, e la velocità G alla quale il mobile B percorre lo spazio T nel tempo R, mentre il rapporto C a G è composto dal prodotto dei rapporti C a E e E a G; l’altro rapporto C a E è posto allo stesso modo del rapporto tra lo spazio V e lo spazio T; il rapporto E a G è invero lo stesso del rapporto R a S: è così dunque spiegata la proposizione.

DE MOTU NATURALITER ACCELERATO.

Quae in motu aequabili contingunt accidentia, in praecedenti libro considerata sunt: modo de motu accelerato pertractandum.

Et primo, definitionem ei, quo utitur natura, apprime congruentem investigare atque explicare convenit. Quamvis enim aliquam lationis speciem ex arbitrio confingere, et consequentes eius passiones contemplari, non sit inconveniens (ita, enim, qui helicas aut conchoides lineas ex motibus quibusdam exortas, licet talibus non utatur natura, sibi finxerunt, earum symptomata ex suppositione demonstrarunt cum laude), tamen, quandoquidem quadam accelerationis specie gravium descendentium utitur natura, eorundem speculari passiones decrevimus, si eam, quam allaturi sumus de nostro motu accelerato definitionem, cum essentia motus naturaliter accelerati congruere contigerit. Quod tandem, post diuturnas mentis agitationes, repperisse confidimus; ea potissimum ducti ratione, quia symptomatis, deinceps a nobis demonstratis, apprime respondere atque congruere videntur ea, quae naturalia experimenta sensui repraesentant. Postremo, ad investigationem motus naturaliter accelerati nos quasi manu duxit animadversio consuetudinis atque instituti ipsiusmet naturae in ceteris suis operibus omnibus, in quibus exercendis uti consuevit mediis primis, simplicissimis, facillimis. Neminem enim esse arbitror qui credat, natatum aut volatum simpliciori aut faciliori modo exerceri posse, quam eo ipso, quo pisces et aves instinctu naturali utuntur.
Dum igitur lapidem, ex sublimi a quiete descendentem, nova deinceps velocitatis acquirere incrementa animadverto, cur talia additamenta, simplicissima atque omnibus magis obvia ratione, fieri non credam? Quod si attente inspiciamus, nullum additamentum, nullum incrementum, magis simplex inveniemus, quam illud, quod semper eodem modo superaddit. Quod facile intelligemus, maximam temporis atque motus affinitatem inspicientes: sicut enim motus aequabilitas et uniformitas per temporum spatiorumque aequabilitates definitur ac concipitur (lationem, enim, tunc aequabilem appellamus, cum temporibus aequalibus aequalia conficiuntur spatia), ita per easdem aequalitates partium temporis, incrementa celeritatis simpliciter facta percipere possumus; mente concipientes, motum illum uniformiter eodemque modo continue acceleratum esse, dum temporibus quibuscumque aequalibus aequalia ei superaddantur celeritatis additamenta. Adeo ut, sumptis quotcumque temporis particulis aequalibus a primo instanti in quo mobile recedit a quiete et descensum aggreditur, celeritatis gradus in prima cum secunda temporis particula acquisitus, duplus sit gradus quem acquisivit mobile in prima particula; gradus vero quem obtinet in tribus temporis particulis, triplus; quem in quatuor, quadruplus eiusdem gradus primi temporis: ita ut (clarioris intelligentiae causa), si mobile lationem suam continuaret iuxta gradum seu momentum velocitatis in prima temporis particula acquisitae, motumque suum deinceps aequabiliter cum tali gradu extenderet, latio haec duplo esset tardior ea, quam iuxta gradum velocitatis in duabus temporis particulis acquisitae obtineret. Et sic a recta ratione absonum nequaquam esse videtur, si accipiamus, intentionem velocitatis fieri iuxta temporis extensionem; ex quo definitio motus, de quo acturi sumus, talis accipi potest: Motum aequabiliter, seu uniformiter, acceleratum dico illum, qui, a quiete recedens, temporibus aequalibus aequalia celeritatis momenta sibi superaddit.

———————-

SUL MOTO NATURALMENTE ACCELERATO

I casi che riguardano il moto equabile sono stati considerati nel precedente libro: ora è da trattare del moto accelerato.

conviene perciò come prima cosa ricercare e spiegare innanzi tutto la definizione che esattamente corrisponde a ciò di cui la natura dà prova. Sebbene, in realtà, non sia sconveniente fissare arbitrariamete qualche specie di movimento, e di questo considerarne le conseguenti particolarità (è così, infatti, che coloro che s’immaginarono linee spirali o concoidi, venute fuori da certi movimenti, riuscirono lodevolmente a dimostrarne le proprietà per via di supposizione, nonostante di tali moti la natura non desse affatto prova), tuttavia, dal momento che la natura dà prova di un certo tipo di accelerazione per i gravi discendenti, abbiamo stabilito di indagarne le particolarità, posto che alla definizione che ci avviamo a dare del nostro moto accelerato tocchi di coincidere con l’essenza del moto naturalmente accelerato. La qual cosa, finalmente, dopo durevoli riflessioni, riteniamo di aver raggiunto. Soprattutto per la ragione che le proprietà da noi di seguito evidenziate, sembrano esattamente corrispondere e coincidere con ciò che gli esperimenti naturali presentano ai sensi. In ultimo, allo studio del moto naturalmente accelerato siamo stati condotti quasi per mano dall’osservazione della consuetudine e della regola seguite dalla natura medesima in tutte le altre sue opere, nella cui attuazione suole giovarsi delle soluzioni più immediate, più semplici e più facili. Ritengo infatti che non ci sia nessuno il quale creda che si possa praticare il nuoto o il volo in una maniera più semplice e più facile di quella usata per proprio istinto naturale dai pesci e dagli uccelli. Quando dunque osservo che una pietra, discendendo dall’alto a partire dalla quiete, acquista via via nuovi incrementi di velocità, perché non dovrei credere che tali aumenti avvengano secondo la più semplice e la più ovvia proporzione? Per cui, se consideriamo attentamente la cosa, non troveremo nessun aumento o incremento più semplice di quello che si accresce sempre nel medesimo modo. Il che facilmente intenderemo, considerando la stretta connessione tra tempo e moto: come infatti l’equabilità e uniformità del moto si definisce e si concepisce in base all’eguaglianza dei tempi e degli spazi (chiamiamo infatti equabile il moto, allorché in tempi eguali vengono percorsi spazi uguali), così, mediante le medesime uniformi suddivisioni del tempo, possiamo concepire che in modo altrettanto semplice si producano gli incrementi di velocità; concependo in astratto che quel moto sia uniformemente e, nella stessa maniera, continuamente accelerato, fintanto che in tempi eguali, qualsiasi essi siano, ad esso si aggiungano eguali aumenti di velocità. Nella stessa misura, per frazioni eguali di tempo in qualsiasi numero prese, dal primo istante in cui il mobile abbandona la quiete e comincia a scendere, il grado di velocità acquistato nella prima e seconda frazione di tempo prese insieme, sia doppio rispetto al grado acquistato dal mobile nella prima frazione; e il grado che poi si ottiene in tre frazioni di tempo, sia triplo; quello acquistato in quattro, quadruplo del medesimo grado del primo tempo: così che (per una più chiara comprensione), se il mobile continuasse il suo moto secondo il grado o momento di velocità acquistato nella prima frazione di tempo, e uniformemente lo proseguisse con tale grado, questo moto sarebbe due volte più lento di quello che [il mobile] otterrebbe secondo il grado di velocità acquistato in due frazioni di tempo. E così non ci sembra affatto di discordare dalla retta ragione se ammettiamo che l’intensità della velocità si accresce secondo l’estensione del tempo; da cui si può ammettere la seguente definizione del moto di cui stiamo per trattare: definisco moto equabilmente, ossia uniformemente, accelerato, quello che, abbandonando la quiete, in tempi eguali aggiunge a sé [acquista] eguali momenti di velocità.